迈克耳孙-莫雷实验
-
迈克,耳孙,莫雷,实验,原文,标题,迈克,耳孙,
- 中国历史人物-小虎历史故事网
- 2023-04-13 00:09
- 小虎历史故事网
迈克耳孙-莫雷实验 ,对于想了解历史故事的朋友们来说,迈克耳孙-莫雷实验是一个非常想了解的问题,下面小编就带领大家看看这个问题。
原文标题:迈克耳孙-莫雷实验
实验原理实验装置当时认为光的传播介质中国历史人物类传记电影
是“以太”。由此产生了一个新的问题:地球以每秒30公里的速度绕太阳运动,就必须会遇到每秒30公里的“以太风”迎面吹来,同时,它也必须对光的传播产生影响。这个问题的产生,引起人们去探讨“以太风”存在与否。迈克耳孙中国历史人物中国地图轮廓
-莫雷实验就是在这个基础上进行的。当“以太风”的速度为0时,两束光应同时到达,因而相位相同;如“以太风”速度不为零,即装置相对以太运动,则两列光波相位不同。假设装置在以太中向右以速度v{\displaystylev}运动,且从部分镀银的玻璃片到两面镜子的距离为L{\displaystyleL},那么向右的那一束光在向右的过程中相对装置速度为c−−-->v{\displaystylec-v},花费的时间t1=L/(c−−-->v){\displaystylet_{1}=L/(c-v)},返回时速度为c+v{\displaystylec+v},时间t2...实验原理
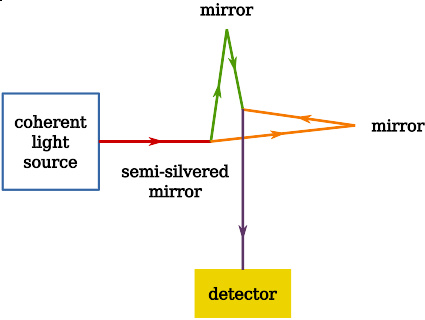
迈克耳孙-莫雷实验
实验装置
当时认为光的传播介质是“以太”。由此产生了一个新的问题:地球以每秒30公里的速度绕太阳运动,就必须会遇到每秒30公里的“以太风”迎面吹来,同时,它也必须对光的传播产生影响。这个问题的产生,引起人们去探讨“以太风”存在与否。迈克耳孙-莫雷实验就是在这个基础上进行的。
当“以太风”的速度为0时,两束光应同时到达,因而相位相同;如“以太风”速度不为零,即装置相对以太运动,则两列光波相位不同。
假设装置在以太中向右以速度 v {\displaystyle v} 运动,且从部分镀银的玻璃片到两面镜子的距离为 L {\displaystyle L} ,那么向右的那一束光在向右的过程中相对装置速度为 c − − --> v {\displaystyle c-v} ,花费的时间 t 1 = L / ( c − − --> v ) {\displaystyle t_{1}=L/(c-v)} ,返回时速度为 c + v {\displaystyle c+v} ,时间 t 2 = L / ( c + v ) {\displaystyle t_{2}=L/(c+v)} 。所以总的时间是
t 1 + t 2 = 2 L c c 2 − − --> v 2 = 2 L c ⋅ ⋅ --> ( 1 − − --> v 2 / c 2 ) {\displaystyle t_{1}+t_{2}={\frac {2Lc}{c^{2}-v^{2}}}={\frac {2L}{c\cdot (1-v^{2}/c^{2})}}}
而对于向上的那一束光,设它到达镜子所需的时间为 t 3 {\displaystyle t_{3}} ,在这段时间里镜子向右移动了 v t 3 {\displaystyle vt_{3}} ,
中国历史朝代春秋历史人物
所以光走过的路程是一个直角三角形的斜边,于是有L 2 = ( c t 3 ) 2 − − --> ( v t 3 ) 2 = ( c 2 − − --> v 2 ) t 3 2 {\displaystyle L^{2}=(ct_{3})^{2}-(vt_{3})^{2}=(c^{2}-v^{2})t_{3}^{2}}
由此可得 t 3 = L c 2 − − --> v 2 {\displaystyle t_{3}={\frac {L}{\sqrt {c^{2}-v^{2}}}}}
而返回时间与此相同,所以总时间 2 t 3 = 2 L c 2 − − --> v 2 = 2 L c ⋅ ⋅ --> 1 − − --> v 2 / c 2 {\displaystyle 2t_{3}={\frac {2L}{\sqrt {c^{2}-v^{2}}}}={\frac {2L}{c\cdot {\sqrt {1-v^{2}/c^{2}}}}}}
所以两束光的到达时间是不同的,根据这个实验应该能测量出地球通过以太的速度。

迈克耳孙-莫雷实验
红色激光造成的迈克耳孙干涉环
空气介质的影响
由于实验是在空气介质中进行,此时光的介质相对于实验装置的速度为0, 所以在两个路径上的来回的时间均为2l/c。 因此,在装置旋转90°后,没有干涉条纹的移动。
实验结果
莫雷不确信他自己的结论,继续与达通·米勒做更多的实验。米勒制作了更大的实验设备,最大的安装于威尔逊山天文台的臂长32米(有效长度)的仪器。为了避免实体墙可能造成的对以太风的阻挡,他使用了帆布为主体的流动墙。他每次旋转设备都会观测到不同的小偏移,不论是恒星日还是年。他的测量值仅达到~10 km/s,而不是从地球轨道运动所期待的~30 km/s。他仍然不确信这是由于局部拖拽造成的,他没有尝试进行详细的解释。
肯尼迪后来在威尔逊山上作了实验,米勒发现1/10的漂移,并且不受季节影响。米勒的发现当时认为非常重要,并于1928年在一份会议报告上与迈克耳孙、洛伦兹等人讨论。普遍认为需要更多的实验来检验米勒的结果。洛伦兹认可这个结论,造成漂移的原因不符合他的以太说或者爱因斯坦的狭义相对论。爱因斯坦没有出席会议,但是感觉这个实验结果恐怕是实验误差。后来的实验没能重新获得米勒的结果,现代实验的精度推翻了此实验结论。
近代实验
近代版的迈克耳孙-莫雷实验变得司空见惯。激光和激微波通过让光线在充满高能原子的精心调整的空间内来回反射,以放大光线。这样的有效长度可达千米。还有一个好处,同一光源在不同光线角度产生同样的相位,给干涉计增加了额外精确度。
第一个这样的实验是由查尔斯·H·汤斯(Charles H. Townes)做的,第一个激微波制作者之一。他们1958年的实验把漂移的上限,包括可能的实验误差,降低到仅仅30m/s。在1974年通过三角形内修剪工具精确的激光重复实验把这个值降低到0.025m/s,并且在一个光臂上放上玻璃来测试拖拽效果。在1979年Brillet-Hall实验把人以方向的上限降低到30m/s,但是双向因素降低到0.000001 m/s (i.e.,静止或者夹带以太)。Hils和Hall在经过一年的重复实验之后,于1990年公布,各向异性的极限降低到2×10。
实验结果证明,不论地球运动的方向同光的射向一致或相反,测出的光速都相同,在地球同设想的“以太”之间没有相对运动。当时迈克耳孙因此认为这个结果表明以太是随着地球运动的。
对实验结果的解释
乔治·斐兹杰惹(George FitzGerald)在1892年对迈克耳孙-莫雷实验提出了一种解释。他指出如果物质是由带电荷的粒子组成,一根相对于以太静止的量杆的长度,将完全由量杆粒子间取得的静电平衡决定,而量杆相对于以太在运动时,量杆就会缩短,因为组成量杆的带电粒子将会产生磁场,从而改变这些粒子之间的间隔平衡。这一来,迈克耳孙-莫雷实验所使用的仪器,当它指向地球运动的方向时就会缩短,而缩短的程度正好抵消光速的减慢。
有些人曾经试行测量乔治·斐兹杰惹的缩短值,但都没有成功。这类实验表明乔治·斐兹杰惹的缩短,在一个运动体系内是不能被处在这个运动体系内的观察者测量到的,所以他们无法判断他们体系内的绝对速度,光学的定律和各种电磁现象是不受绝对速度的影响的。再者,动系中的短缩,乃是所有物体皆短缩,而动系中的人,是无法测量到自己短缩值的。
1904年,荷兰物理学家洛伦兹提出了著名的洛伦兹变换,用于解释迈克耳孙-莫雷实验的结果。他提出运动物体的长度会收缩,并且收缩只发生运动方向上。如果物体静止时的长度为 L 0 {\displaystyle L_{0}} ,当它以速度 v {\displaystyle v} 以平行于长度的方向运动时,长度收缩为
L = L 0 ⋅ ⋅ --> 1 − − --> v 2 / c 2 {\displaystyle L=L_{0}\cdot {\sqrt {1-v^{2}/c^{2}}}}
引入这条规律后 t 1 + t 2 = 2 L ⋅ ⋅ --> 1 − − --> v 2 / c 2 c ⋅ ⋅ --> ( 1 − − --> v 2 / c 2 ) = 2 L c ⋅ ⋅ --> 1 − − --> v 2 / c 2 = 2 t 3 {\displaystyle t_{1}+t_{2}={\frac {2L\cdot {\sqrt {1-v^{2}/c^{2}}}}{c\cdot (1-v^{2}/c^{2})}}={\frac {2L}{c\cdot {\sqrt {1-v^{2}/c^{2}}}}}=2t_{3}} ,成功地解释了实验结果。(参见:洛伦兹变换)
1905年,爱因斯坦在抛弃以太、以光速不变原理和狭义相对性原理为基本假设的基础上建立了狭义相对论。狭义相对论认为空间和时间并不相互独立,而是一个统一的四维时空整体,并不存在绝对的空间和时间。在狭义相对论中,整个时空仍然是平直的、各向同性的和各点同性的。结合狭义相对性原理和上述时空的性质,也可以推导出洛伦兹变换。
里茨在1908年设想光速是依赖于光源的速度的,企图以此解释迈克耳孙-莫雷实验
中国历史人物英语内容简介
。但是德·希特于1931年在莱顿大学指出,如果是这样的话,那么一对相互环绕运动的星体将会出现表观上的异常运动,而这种现象并没有观察到。由此也证明了爱因斯坦提出的光速和不受光源速度和观察者的影响是正确的,而且既然没有一种静止的以太传播光波振动,牛顿关于光速可以增加的看法就必须抛弃。有人认为,爱因斯坦在提出狭义相对论的过程
中国历史人物高清图
中,曾经受到过迈克耳孙-莫雷实验结果的影响。John Stachel在《爱因斯坦和以太漂移实验》一文中指出,有间接的有力证据表明,爱因斯坦在1889年一定知道迈克耳孙-莫雷实验,并从1889~1901年间,持续感兴趣于设计光学实验,以检查地球穿行于以太的假定运动。爱因斯坦在1922年,在《我是怎样创造了相对论》中说道:“那时我想用某种方法演示地球相对以太的运动……,在给自己提出这一问题时,我没有怀疑过以太的存在和地球的运动。于是,我预料如果把光源发出的光线用镜子反射,则当它的传播方向是平行或反平行于地球的运动方向时,应该具有不同的能量。所以我提出使用两个热电偶,利用测量它们所生热量的差值,来证实这一点。”
对实验结果的再验证
1893年洛奇在伦敦发现,光通过两块快速转动的巨大钢盘时,速度并不改变,表明钢盘并不把以太带着转。对恒星光行差的观测也显示以太并不随着地球转动。
人们在不同地点、不同时间多次重复了迈克耳孙-莫雷实验,并且应用各种手段对实验结果进行验证,精度不断提高。除光学方法外,还有使用其他技术进行的类似实验。如1958年利用微波激射所做的实验得到地球相对以太的速度上限是3×10 km/s,1970年利用穆斯堡尔效应所做的实验得到此速度的上限只有5×10 km/s。综合各种实验结果,人们基本可以判定地球不存在相对以太的运动。
参阅
迈克耳孙干涉仪
移动中的磁铁与导体问题
狭义相对论发现史
参考文献
引文注释
免责声明:以上内容版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。感谢每一位辛勤著写的作者,感谢每一位的分享。
原文出处:http://www.cnlishi.cn/news/11726.html
以上是关于迈克耳孙-莫雷实验的介绍,希望对想了解历史故事的朋友们有所帮助。
本文标题:迈克耳孙-莫雷实验;本文链接:https://gazx.sd.cn/zgrw/3462.html。
猜你喜欢
- 中国历史人物谁有耳孙的故事、关于耳的典故 2025-12-02
- 中国历史人物谁有耳孙的、鼻祖叫耳孙什么 2025-12-02
- nba历史名人排行榜 nba历史明星排名 2025-06-22
- 迈克尔·波特 2023-07-18
- 迈克尔·贝 2023-06-28
- 迈克·毕比-迈克·毕比简介,后代,族谱 2023-06-17
- 迈克尔·波顿-迈克尔·波顿简介,后代,族谱 2023-05-26
- 篮球-鲍勃·麦卡杜 2023-05-25
- 拉尔夫·舒马赫-拉尔夫·舒马赫 2023-05-18
- 迈克·华莱士 2023-05-18



















