秦九韶

秦九韶 ,对于想了解历史故事的朋友们来说，秦九韶是一个非常想了解的问题，下面小编就带领大家看看这个问题。

原文标题：秦九韶

生平秦九韶的籍贯是鲁郡（今山东省济宁市兖州区、曲阜一带），祖上世代为官。父亲秦季槱（yǒu／ㄧㄡˇ）字宏父，是四川普州（现安岳县）人，曾知潼州府、任职秘阁。1208年，秦九韶生于普州，（今四川安岳）是家里的第二个儿子。嘉定五年（1212年），秦季槱任巴州知州。嘉定十二年（1219年），兴元军士权兴等叛乱，秦季槱守巴州失陷，秦九韶随父亲回到临安（今杭州）。嘉定十五年后，秦季槱擢升工部郎中、秘书少监兼国史院编修官、实录检讨官。由于父亲是掌管各项工程、屯田、水利、交通的工部郎中，又任国史院官职，掌管各类经籍图书，少年的秦九韶得以接触学习各类知识。他生性聪颖，对当时的种种学问，如星象、音乐、算术以及建筑学等无一不学，并专研甚深。他还曾经向当时的隐士求教，学习数学。十八岁时在乡里为义兵首领。绍定二年（1229年）十月，秦九韶擢郪县县尉。绍定五年（1232）八月乙丑进士。端平三年（1236年）一月，秦...

生平

秦九韶的籍贯是鲁郡（今山东省济宁市兖州区、曲阜一带），祖上世代为官。父亲秦季槱（yǒu／ㄧㄡˇ）字宏父，是四川普州（现安岳县）人，曾知潼州府、任职秘阁。1208年，秦九韶生于普州 ，（今四川安岳）是家里的第二个儿子。嘉定五年（1212年），秦季槱任巴州知州。嘉定十二年（1219年），兴元军士权兴等叛乱，秦季槱守巴州失陷，秦九韶随父亲回到临安（今杭州）。嘉定十五年后，秦季槱擢升工部郎中、秘书少监兼国史院编修官、实录检讨官。由于父亲是掌管各项工程、屯田、水利、交通的工部郎中，又任国史院官职，掌管各类经籍图书，少年的秦九韶得以接触学习各类知识。他生性聪颖，对当时的种种学问，如星象、音乐、算术以及建筑学等无一不学，并专研甚深。他还曾经向当时的隐士求教，学习数学 。

十八岁时在乡里为义兵首领 。绍定二年（1229年）十月，秦九韶擢郪县县尉 。绍定五年（1232）八月乙丑进士 。端平三年（1236年）一月，秦九韶擢升湖北蕲州（今湖北蕲春县）通判 。嘉熙元年（1237年）秋，秦九韶知和州（今安徽和县）。嘉熙二年（1238年），秦季槱逝世，秦九韶回临安吊丧。吊丧期间曾在杭州西溪上设计修建一座桥，后来被朱世杰命名为“道古桥” 。

南宋理宗淳祐四年（1244年）八月，秦九劭在建康府（今江苏江宁县）做官（通直郎），十一月因母去世离任，回浙江湖州吊丧 。在此期间，他将自己潜心研究的各种实践中的数学成果集撰成书。淳祐七年（1247年）九月，在湖州完成了《 数书九章 》（当时称为《数学大略》）十八卷，自述“历岁遥塞，荏苒十禩”。宝祐二年（1254年）到建康出任沿江制置司参议 ，宝祐六年（1258年）出任琼州守，南宋理宗景定元年（1260年）出任梅州（今广东梅县）守，后卒于

梁衡 点评中国历史人物

梅州 。《宋史》无传。

成就

秦九韶的数学成就基本表现在他写的《数书九章》之中。然而，这本书在当时并没有引起大的影响，稍后的杨辉、朱世杰都没有引征过秦九韶的成果 。《数书九章》的主要内容偏重于数学的应用方面，全书八十一道题目都是结合当时的实际需要提出的问题。

大衍求一术

大衍求一术是一次同余方程组问题的核心解法，现在叫做中国剩余定理。一次同余方程组问题的求解始于《孙子算经》中的“今有物不知数”问题。例如《孙子算经》中的原题是：

用现代的数学语言表述一般的“物不知数”问题，就是：

在《数书九章》第一卷的“大衍总术”中，秦九韶将 m 1 , m 2 , … … --> , m n {\displaystyle m_{1},m_{2},\ldots ,m_{n}} 称为 定数 ，将它们的总乘积 M = m 1 m 2 , … … --> m n {\displaystyle M=m_{1}m_{2},\ldots m_{n}} 称为 衍母 ，再将衍母除以各个定数所得到的商： M i = M m i {\displaystyle M_{i}={\frac {M}{m_{i}}}} 称为 衍数 。接下来他将满足 k i M i ≡ ≡ --> 1 ( mod m i ) {\displaystyle k_{i}M_{i

西方颠覆中国历史人物是谁

}\equiv 1{\pmod {m_{i}}}} 的正整数 k i {\displaystyle k_{i}} 称为 乘率 ，只要知道了各个乘率 k i {\displaystyle k_{i}} ，就可以得到方程组的解：

而计算乘率的方法就是 大衍求一术 。秦九韶完整地叙述了“大衍求一术”，其实质是辗转相除法的应用。于是，针对同余模数两两互素的情况，秦九韶得到了系统的解法，在模数不是两两同余时，需要将定数修正（剔除公因数）以应用大衍求一术。由于没有素因数分解的概念，秦九韶用了一些技巧来修正定数以使用大衍求一术 。

1801年，高斯系统地解决了一元不定方程组的问题，其方法和秦九韶是一样的。

秦九韶算法

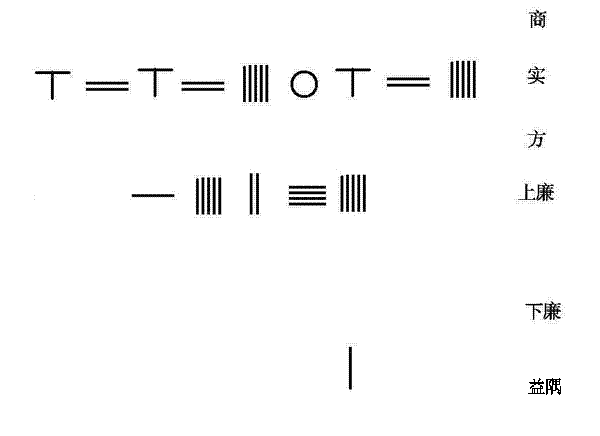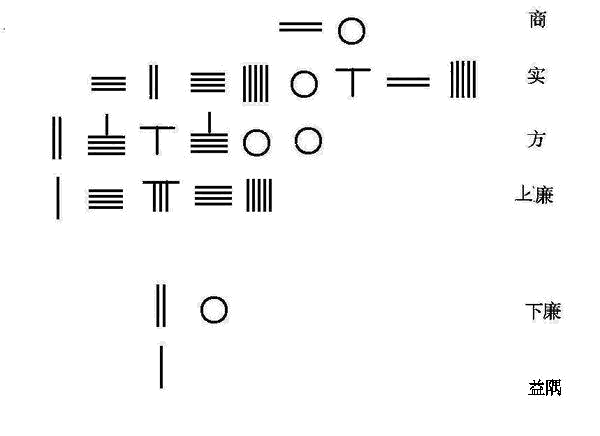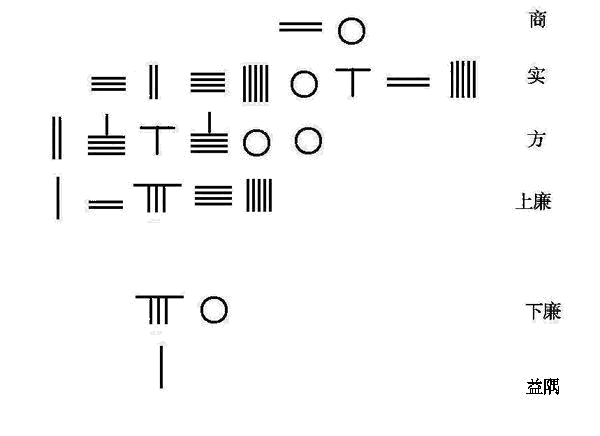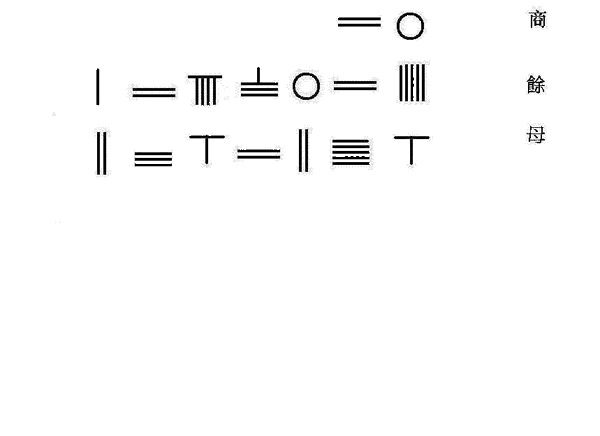
秦九韶解 − − --> x 4 + 15245 x 2 − − --> 6262506.25 {\displaystyle -x^{4}+15245x^{2}-6262506.25}

中国历史人物传记大系

秦九韶算法是一个求一元高次方程的数值解的通用算法，是对贾宪的增乘开方术的改进。13世纪，中国数学家关于开方术的著作很多，但大多散佚，而现传于世的李冶和朱世杰的著作中并没有开方的详细演算步骤。因此，《数书九章》中的“正负开方术”是了解当时解高次方程方法的重要依据 。在《数书九章》中，开方法得到极大完善，利用随乘随加的方法得到方程的根。秦九韶的算法中规定“实常为负”。这里的“实”指的是方程中常数项的系数。实际上，秦九韶将方程写作 f ( x ) = 0 {\displaystyle f(x)=0} ，以便统一解决，这是以

中国历史人物圣号

往的开方术中没有的。所求的方根是无理数时，刘徽曾经首创继续开方，用十进小数来近似表示方程的根的方法。然而这种方法并没有得到后人的重视，直到秦九韶重新采取这种方法 。

三斜求积术

《数书九章》第五卷有“三斜求积”一题。其中“三斜”为“大斜”、“中斜”、“小斜”，是三角形从大到小的三条边。秦九韶列出的面积公式是：

这个公式和海伦公式是等价的。A>C>B

注释

^ 李俨、钱宝琮认为秦九韶生于1202年，但现今数学史界普遍认为是1208年。

参见

《数书九章》

中国剩余定理

增乘开方术

秦九韶算法

免责声明：以上内容

中国历史人物视频下

版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。感谢每一位辛勤著写的作者，感谢每一位的分享。

原文出处：http://www.cnlishi.cn/news/10122.html

以上是关于秦九韶的介绍，希望对想了解历史故事的朋友们有所帮助。

本文标题：秦九韶；本文链接：http://gazx.sd.cn/zgrw/5062.html。