張家山漢簡《算數書》“睘材”試釋
-
張家,山,漢簡,《,算數書,》,“,睘材,”,試釋,
- 中国历史故事-小虎历史故事网
- 2023-08-29 20:03
- 小虎历史故事网
張家山漢簡《算數書》“睘材”試釋 ,对于想了解历史故事的朋友们来说,張家山漢簡《算數書》“睘材”試釋是一个非常想了解的问题,下面小编就带领大家看看这个问题。
原文标题:張家山漢簡《算數書》“睘材”試釋
(南京師範大學歷史系)
張家山漢簡《算數書》“睘材”題因爲原簡字迹難辨之處太多,造成原釋文中有許多缺文,因而至今沒有令人滿意的釋讀。筆者將原簡字迹難辨處加以處理,從中得到關鍵綫索,幷得到自覺滿意的釋讀,今公布于此,以就教于方家。
《算數書》“睘材”題含156、158號兩支簡,張家山二四七號漢墓竹簡整理小組的釋文爲:
睘(圜)材 有圜材一(?),斷之囗囗市囗囗囗囗囗囗囗大幾何?曰:七(?)十(?)六(?)囗囗四寸半寸。述(術)曰:囗自乘,以(156)
入二寸益之,即大數已[1]。(158)
由于很多文字無法釋讀,本題諸家均無法讀通[2]。筆者對原簡圖版進行一定程度的技術處理,使一些關鍵字得以讀出,部分圖版處理結果貼出如下[3]:

張家山漢簡《算數書》“睘材”試釋

張家山漢簡《算數書》“睘材”試釋

張家山漢簡《算數書》“睘材”試釋

張家山漢簡《算數書》“睘材”試釋

張家山漢簡《算數書》“睘材”試釋
圖1:有圜材一 圖2:斲之入二寸 圖3:平尺四寸 圖4:曰大二尺有 圖5:六寸半寸
從圖1可知,“圜材”之後還有餘地,幷有墨迹,因此,原釋文“一”字可取。從圖2可以看到,原釋文“斷之囗囗市”是成問題的,對比“斷”字的寫法可以發現,此段竹簡的第一個字左上有二小“口”字形,其形比“斷”之小“口”明顯要大,而其下既沒有“斷”字那
电影 中国历史故事
麽多筆劃的墨迹,最左側幷無“斷”字之“∟”形之殘墨,空間也不足以容納“斷”字的左下部。因此這個字不是“斷”字,而應該是“斲”字。綜合字迹及圖2其他簡文可以發現此字確爲“斲”字,而此段簡文爲“斲之入二寸”。“斲”與“斷”一字之差,却關係到全題的理解與釋讀。岳麓書院藏秦簡《數》書以及《九章算術•勾股》都有“斲圜材”的算題,其文援引如下:
[今]有圓材薶[埋]地,不智[知]小大,斲之,入材一寸而得平一尺,問材周大幾(可)[何]?即曰:半平得五寸,令相乘也,以深一寸爲法,如法得一寸。有[又]以深益之,即材徑也[4]。
今有圓材,埋在壁中,不知大小。以鋸鋸之,深一寸,鋸道長一尺。問徑幾何?荅曰:材徑二尺六寸。
術曰:半鋸道自乘,如深寸而一,以深寸增之,即材徑[5]。
本算題所論是“圜材”,簡文有“斲之入二寸”句,幷且“而得”、“問囗大幾何”、“寸自乘”、以及“入二寸益之”都可以明確釋讀,在簡文中又都處于合適的位置。因此,對比以上所引二題,本題毫無疑問是一個同類的“斲圜材”算題。
圖3所示竹簡片段第一字無法辨認,第二字的位置依上下文及墨迹形狀應是“尺”字,第三字依墨迹形狀應爲“六”或者“四”字。最後一字則是“寸”字。此段竹簡之前有“而得”二字,其中“而”字可辨,“得”字依上下文可以斷定。對照岳麓書院藏秦簡《數》書相應內容,可以判斷此四字爲“平尺四寸”或“平尺六寸”。
圖4、圖5兩部分,原釋文爲“曰七(?)十(?)六(?)”及“囗囗四寸半寸”。據圖5,“寸半寸”可辨,而第一字依殘墨判斷,或者如原釋文是“四”字,或者是“六”字。圖4除“曰”字外均不可辨,但依上下文知其爲“曰大囗尺囗”。考慮圖5簡文是“囗寸半寸”,而“尺”後面的字殘墨之迹與“有”近似,故依行文此應爲“有[又]”字。至此,據計算可知,此答數爲“二尺有六寸半寸”
中国历史成语故事演讲稿
,而圖3則爲“平尺四中国历史上的故事图片大全
寸”。對照上引岳麓秦簡的行文“術”文,可知158號簡脫漏“爲法,又以入二寸”七個字。因爲“入二寸”在原簡此段簡文中兩見,這一脫誤的原因是明顯的:它因簡文上下兩處“入二寸”相涉而産生。至此,我
中国历史故事常识积累
們得到原簡的簡文如下:睘材 有圜〖材〗一,斲之入二寸,而得〖平尺四〗寸,問〖徑〗大幾何?曰:大〖二尺有六〗寸半寸。述[術]曰:〖七〗寸自乘,以(156)
入二寸【爲法,又以入二寸】益之,即大數已。(158)
此處,158簡中的“大”即問題中的“材大”,“大數”即爲圓材直徑之尺寸數。《九章算術》將此類算題歸入“勾股”章,其計算公式由勾股定理推導而得,其推導過程如下:
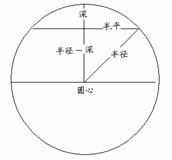
張家山漢簡《算數書》“睘材”試釋
如上圖,(半徑-深)、半平、半徑 構成直角三角形,據勾股定理得:
(半徑-深)×(半徑-深)+半平×半平=半徑×半徑
展開、化簡,得:
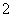
張家山漢簡《算數書》“睘材”試釋
因此,
直徑=半平×半平/深+深
本題、上引岳麓秦簡、《九章算術》三者算法的叙述方式相互均有所不同,但都是以上這個公式。按照這個公式,本題的計算如下:
圜材直徑
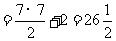
張家山漢簡《算數書》“睘材”試釋
(編者按:[1]參見:張家山二四七號漢墓竹簡整理小組:《張家山漢墓竹簡[二四七號墓](釋文修訂本)》,文物出版社,2006年5月,第153頁。按:整理小組將157號簡歸入此題,不確,爲簡化討論,此處徑略去此簡。
[2]彭浩:《張家山漢簡〈算數書〉注釋》,科學出版社,2001年,第113頁;郭世榮:《〈算數書〉勘誤》,《內蒙古 大學學報(自然科學版)》,2001年第3期;郭書春:《〈算數書〉校勘》,《中國科技史料》,2001年第3期。
[3]張家山二四七號漢墓竹簡整理小組:《張家山漢墓竹簡[二四七號墓]》,文物出版社,2001年11月,第96頁,156號簡。
[4]參見:肖燦、朱漢民:《岳麓書院藏秦簡〈數〉的主要內容及歷史價值》,《中國史研究》,2009年第3期。
[5]參見:李繼閔:《〈九章算術〉導讀與譯注》,陝西科學技術出版社,1998年9月,第695-697頁。 (责任编辑:admin)
原文出处:http://his.newdu.com/a/201711/05/513866.html
以上是关于張家山漢簡《算數書》“睘材”試釋的介绍,希望对想了解历史故事的朋友们有所帮助。
本文标题:張家山漢簡《算數書》“睘材”試釋;本文链接:http://gazx.sd.cn/zggs/27100.html。
猜你喜欢
- 汪精卫-汪精卫的坟墓为何会被炸开?这其中有着什么原因? 2023-10-13
- 调虎离山-三十六计之调虎离山的原文意思和故事典故 2023-08-14
- 闻太师-闻太师死了纣王为啥哭了?因为一死江山不报 2023-08-14
- 八大山人-朱耷为什么叫八大山人的名字由来 2023-08-14
- 中国历史上的三个败类(安禄山、洪承畴、汪精卫) 2023-10-13
- 山本五十六-萨沃岛海战,美军死亡人数是日军的20倍,为何山本五十六却大怒 2023-08-11
- 李白-历史上李白长得帅吗(唐朝第一帅诗人,江山英秀,长得不高) 2023-08-11
- 薛灵芸-三国薛灵芸简介:常山绝世美人让曹丕为之倾倒 2023-10-22
- 一百单八将-梁山好汉的习性爱好:水泊梁山的头号色狼是谁? 2023-10-22
- 王母娘娘-解密:古代天庭第一夫人王母娘娘的风流情史 2023-10-22


















