大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
-
大海
- 中国历史故事-小虎历史故事网
- 2023-08-29 15:36
- 小虎历史故事网
大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究 ,对于想了解历史故事的朋友们来说,大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究是一个非常想了解的问题,下面小编就带领大家看看这个问题。
原文标题:嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
(湖南大學嶽麓書院)
摘要:本文敘述了對嶽麓書院藏秦簡《數》的算題【0809+0802】和【2173+0137+0650】的拼綴、編連、研究。這兩例算題內容都與糧米有關。
關鍵詞:秦;簡;數;嶽麓書院;秏程;粟米
秦簡《數》不是通過科學的考古發掘得到的,這使得秦簡《數》缺失了很多的簡文資訊和有關各條之內、各條之間關係的資訊,也缺失了與之相關的墓主個人及其他社會資訊。時代湮遠,古今隔閡,造成了很多疑惑。因此有大量疑難問題,需要通過多方考證才能獲得較為清楚的認識。本文將要討論的是《數》的算題【0809+0802】和【2173+0137+0650】,內容都與糧米有關。
(一) 對算題【0809+0802】的研究
算題【0809+0802】簡文是:秏程。以生
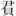
大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
斗之二┕,為之述(術)曰:取一石者十之而以七為法┕,它秏程如此。 0802
1.字詞釋義
秏,同“耗”。《廣韻·号韻》:“秏,減也。俗作耗。”
程[1],計量或計量標準。《漢書·東方朔傳》:“武帝既招英俊,程其器能,用之如不及。”顏師古注:“程,謂量計之也。”秦國至漢代的政府為某些部門和工作制定的數量標準,納入法律的範圍,稱為程。亦用如動詞,表示按程來考量,例如:張家山漢簡《算數書》簡70的“程竹”,簡87的“程它物如此”,簡88的“程禾”。益,增加。《算數書》、《九章算術》多次用“益”。《九章算術》正負術:“異名相益”,益訓加。《廣雅·釋詁二》:“益,加也。”
秏程,或可能為題名。《數》的算題大多無題名。

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
石,簡文的石是容量單位,禾一石為

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
關於“石”的標準參見以下文獻:
(1)《睡虎地秦墓竹簡·倉律》“〔粟一〕……石六斗大半斗”條及“為粟廿斗”條(釋文註釋第二九和三〇頁)。
《算數書》“程禾”條,以及鄒大海先生和彭浩先生的校釋。
(2) 彭浩. 睡虎地秦墓竹簡《倉律》校讀(一則). 北京大學考古文博學院編. 考古學研究(六):慶祝高明先生八十壽辰暨從事考古研究五十年論文集. 北京:科學出版社,2006.499-502
(3) 鄒大海. 從《算數書》和秦簡看上古糧米的比率. 自然科學史研究,2003,(4): 318-328
(4)鄒大海. 出土《算數書》校釋一則. 東南文化. 2004,(2):83-85
又正確版本見:簡帛研究網,http://www.jianbo.org/admin3/html/zhoudahai02. htm,2004-4-11
(5)鄒大海. 關於《算數書》、秦律和上古糧米計量單位的幾個問題. 內蒙古師範大學學報(自然科學漢文版),2009,38(5):508-515
2.算法分析
術文的算法相當於:
大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
這是不完整的,實際計算中應包含這樣的計算步驟:

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
鄒大海先生認為這個計算方法存在問題[2]。由10斗禾舂出7斗米,出米率就遠高于由粟舂出糲米的比例

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
(二) 對算題【2173+0137+0650】的研究
算題【2173+0137+0650】簡文是:
大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
為法,以十斗乘粟十六斗大半斗為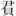
大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究(實)=,(實)如法得粟一斗。 0650
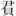
大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
1.簡的編連和復原方案
第0650號簡完整。參照“日本中國古算書研究會”的意見[3],第0650號簡編連入算題。
第2173號簡與第0137號簡可拼綴。斷口契合,內容連貫。拼綴后長度是21.0cm,簡上下仍殘。《數》的完整簡全長多為27.5cm左右,上編繩下緣距離簡首邊緣多為1.5cm左右,下編繩上緣距離簡尾邊緣約1.8cm左右,整簡字數多在38~45字之間。下面復原簡(2173+0137)。
鄒大海先生的意見是[4]:從照片看“粟一石”三字已殘缺大部分,宜先作缺字,再加注說明當作“粟一石”。2173簡在“粟一石”之前殘斷,也不排除殘斷部分還有未知文字的可能性。在0137號簡下段補出“以八斗二升”是符合題意的。 “求粟”和“以八斗二升”之間按照《數》算題的習慣表述可補“之法”,“之術”,“者”等。鄒先生提出六種復原方案:
第一種可能:2173簡“粟一石”前補“稟”字,0137簡後補“者,以八斗二升”字,這時字距較稀了一點。
第二種可能:前簡仍補“稟”字,後簡補“也者,以八斗二升”。
第三種可能,前者補“稟”,後簡補“之法,以八斗二升”。
第四種可能:後簡補“為米者,以八斗二升”。
第五種可能:後簡補“為米一石者,以八斗二升”,這時文字會比較密。
第六種可能:比第五種還多補一個字:“之為米一石者,以八斗二升”
中国历史故事魏征
。總之,什麼情況都有可能,很難判斷哪一種有明顯的優勢。但0137簡末與0650簡相連的文字補作“以八斗二升”是不錯的。

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
圖片說明:以上圖片均為截取的片段。圖片同時提供照片影像(右)和紅外線掃描片影像(左)。紫灰色部份為作者補出的復原方案,補出的圖形文字均采自《數》竹簡。
2.算法分析
我對此題原來的理解是:“禾粟一石為粟谷八斗二升,問糲米一石為禾粟幾何。隱含已知條件“粟率五十,糲米三十”。算式是:

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
“日本「中國
四年级中国历史小故事简短
古算書研究會」”對此題的解釋是[5]:本題和《算數書》的舂粟題一致。題中“粟一石”是指重量一石,對應容量50/3斗。本來從容量50/3斗的粟中能取得10斗的米,現在因損耗只取得8斗2升的米。問若要取得米1石(10斗)需多少粟。比例式是粟50/3斗:米8斗2升=粟X:米10斗。
鄒大海先生對此算題做了詳細解析,他的意見主要有下面幾點[6]:
(1)將《數》的這個算題跟《算數書》的舂粟題比較,這兩個問題有一致性,《數》的這個問題可以用損耗來解釋,但其文本本身和算法本身都未及此。
《算數書》舂粟題,涉及了在標準情況下舂粟時粟和米的數量關係和在有損耗情況下舂粟的數量關係,要求的是在有損耗情況得到一石米時所需要補足的供損耗的粟。其計算過程中,都在術文之外還需要另外計算術文中的參數。而《數》的這個問題,不涉及損耗問題,其術文如果把0137號簡損失文字補上“以八斗二升”(或類似文字)後,則術文提供的算法是完整的。從另一個角度看,雖然從舂粟的標準比例來說,《數》這個問題中一石粟只得八斗二升米,可以用存在損耗來理解,但不管一石粟舂出的米是八斗二升,還是別的什麼數量,只要按正比例關係依術計算出結果來,跟損耗不損耗沒有關係。
(2)《算數書》“舂粟”條中“當益秏粟幾何”前,應脫落了表示已知得到一石米這樣一個已知條件的文字,從秦簡《數》看,這個意見是有根據的,並非古人有這種省略的習慣。但是因為在0809號簡“今有禾,此一石舂之為米七斗,當益禾幾可(何)?”中,也沒有表示已知舂出一石米這個條件的文字,所以《算數書》中“舂粟”省去表示這個條件的文字也是可能的。不過,既然《數》0809的這個題術文不全,答案很可能不對,所以題設被抄錯或改錯的可能性也不小,因此也不能由此認定《數》和《算數書》中表示已知得到一石米的文字沒有出現,一定是一種省略的方式,而不可能是流傳錯誤。
(3)秦簡《數》這個問題的方式為:
在政府的倉儲事務中,由粟舂出的米(糲米)按通常的體積計量方式以十斗為一石,
中国历史故事叫什么名字
粟則按舂出一石米所需要的粟的體積即十六斗大半斗為一石。因此,如果假設秦簡《數》的這個問題以政府的倉儲事務為現實背景,那麼2173+0137簡中“粟中国历史真人故事
一石”就是粟十六斗大半斗,“米一石”即“米十斗”。因此3支簡連在一起形成的整個問題就是:[已知]粟一石(十六斗大半斗)能得到米八斗二升,問要得到一石(十斗)米相應需要多少粟?[答]曰:[粟]廿斗又一百廿三分斗之卌能得到一石(十斗)米。術曰:要求粟[之得一石米者],[以八斗二升]為除數(法),以(一石米的斗數)十斗乘粟(一石的斗數)十六斗大半斗為被除數(實),被除數中有與除數相同的部分就得到一斗(實如法得粟一斗)(或者說被除數除以除數)。
上面方括號內的文字,是為使文意清楚而補足的,圓括號內的文字是解釋性的說明文字。
這個根據現代讀者習慣對問題做的儘量貼近原文的重寫,並不涉及粟米比率5:3,也不涉及損耗數和損耗率。術文列成算式就是:
10斗×

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
這是非常簡單而明確的。這個問題中的粟一石為

大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究
(編者按:[1]“程”的註釋參照彭浩先生的電子郵件修訂。
[2]鄒大海先生對算題【0809+0802】的意見引自鄒大海先生於2010年8月22日的電子郵件
[3]日本「中國古算書研究會」對0650簡的編連意見參照大川俊隆先生於2010年8月19日電子郵件。
[4]鄒大海先生對簡2173、0137的復原意見參照鄒大海先生於2010年8月23日的電子郵件轉述。
[5]“日本「中國古算書研究會」”對算題【2173+0137+0650】的意見參照大川俊隆先生於2010年8月至9月的電子郵件轉述。
[6]鄒大海先生對算題【2173+0137+0650】的意見參照鄒大海先生於2010年8月20日至8月23日的電子郵件轉述。 (责任编辑:admin)
原文出处:http://his.newdu.com/a/201711/05/513996.html
以上是关于大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究的介绍,希望对想了解历史故事的朋友们有所帮助。
本文标题:大海-嶽麓書院藏秦簡《數》兩例與糧米有關的算題研究;本文链接:https://gazx.sd.cn/zggs/27011.html。
猜你喜欢
- 胡大海-胡大海是谁?为什么朱元璋杀了他儿子都不反? 2024-08-28
- 明朝-郑和七下西洋的历史影像:规模最大海上探险(明朝事件) 2024-08-24
- 日德兰-日德兰大海战爆发 2024-06-14
- 大海-大海雀灭绝 2024-06-11
- 朱元璋-朱元璋是如何成就霸业的 2024-05-30
- 炎帝-精卫填海的故事介绍 精卫究竟为何要填海 2024-01-18
- 胡大海-明朝将领胡大海简介 胡大海怎么死的 2024-01-11
- 胡大海-世人对胡大海评价是好是坏 2024-01-10
- 大海-精卫后羿真的是情侣吗 2023-12-28
- 大海-精卫是一只什么样的鸟 精卫填海的故事揭秘 2023-12-28



















