從嶽麓書院藏秦簡《數》看中國早期的衰分問題
-
從嶽,麓書,院藏,秦簡,《,數,》,看中,國,早期,
- 中国历史故事-小虎历史故事网
- 2023-08-30 03:51
- 小虎历史故事网
從嶽麓書院藏秦簡《數》看中國早期的衰分問題 ,对于想了解历史故事的朋友们来说,從嶽麓書院藏秦簡《數》看中國早期的衰分問題是一个非常想了解的问题,下面小编就带领大家看看这个问题。
原文标题:從嶽麓書院藏秦簡《數》看中國早期的衰分問題
(湖南大學嶽麓書院、湖南大學建築學院/嶽麓書院)
比例分配是中國古代數學的一類重要的算法,傳世文獻中《九章算術》專設第三章“衰分”介紹這類算法。“衰分”又叫“差分”,即按比例分配。衰,由大到小依照一定的等級遞減。《管子·小匡》:“相地而衰其政,則民不移矣。”尹知章注:“衰,差也。”李籍云:“以差而平分,故曰衰分。”東漢後期鄭玄引東漢早期鄭眾注《周禮》“九數”時,用後者作“差分”。郭書春認為先秦時“九數”之“差分”,在漢代整理《九章算術》時被換成“衰分”[1]。
在沒有發現秦代數學文獻之前,李儼、錢寶琮、郭書春、鄒大海等學者都認為這類內容在先秦時就已經存在。鄒大海據睡虎地秦律,說明這類方法是戰國時秦國法律所必需,從而這類方法產生和應用於先秦提供了一個時間尺規[2]。嶽麓書院藏秦簡《數》的發現,為我們瞭解中國早期數學提供了大量新的信息,其中保存有較完整(或可推理復原)的“衰分”類算題18例,單獨術文2例,這些實例能檢驗上述觀點,並提供更豐富的認識,現摘引如下[3]:
算題1:衰分之述(術)。耤有五人,此共買鹽一石,一【人出十】錢,一人廿錢,【一】人出卅錢,一人出卌錢,一人出五十錢,今且相去也,欲以錢少【多】(0772)分鹽。其述(術)曰:并五人錢以為法,有(又)各異置【錢】□

從嶽麓書院藏秦簡《數》看中國早期的衰分問題

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
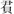
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題2:夫=(大夫)、不更、走馬、上造、公士,共除米一石,今以爵衰分之,各得幾可(何)?夫=(大夫)三斗十五分斗五,不更二斗十五分斗十,走(0978)馬二斗,上造一斗十五分五,公士大半斗。述(術)曰:各直(置)爵數而并以為法,以所分斗數各乘其爵數為
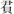
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題3:一牛一羊一犢共食【以】禾一石,問牛羊犢各出幾可(何)?曰:牛五斗有(又)七

從嶽麓書院藏秦簡《數》看中國早期的衰分問題

從嶽麓書院藏秦簡《數》看中國早期的衰分問題

從嶽麓書院藏秦簡《數》看中國早期的衰分問題

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題4:有婦三人,長者一日織五十尺┕,中者二日織五十尺,少者(J09)三日織五十尺,今威有攻(功)五十尺,問各受(J11)幾可(何)?曰:長者受廿七尺十一分尺三┕,中者受十三尺十一分尺七┕,少者受九尺十一分尺一。述(術)曰:各直(置)一日所織(0827)
算題5:

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
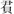
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題6:卒百人,戟十、弩五、負三,問得各幾可(何)?得曰:戟五十五人十分人十,弩廿七人十八分人十四,負十六人十八分人十二。其(0820)述(術)曰:同戟、弩、負數,以為法,即置戟十,以百乘之,以為
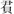
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題7:凡三卿〈鄉〉,其一卿〈鄉〉卒千人,一卿〈鄉〉七百人,一卿〈鄉〉五百人,今上歸千人,欲以人數衰之,問幾可(何)歸幾可(何)? 曰:千者歸四【百】(0943)五十四人有(又)二千二百分人千二百·七百者歸三百一十八人有(又)二千二百分人四百·五百歸二百廿七人有(又)二千二百分人六百。(0856)其述(術)曰:同三卿〈鄉〉卒,以為灋(法),各以卿〈鄉〉卒乘千人為
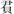
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題8:一人負米十斗,一人負粟十斗,負食十斗,并裹而分之,米、粟、食各取幾可(何)?曰:米取十四斗七分斗二┕,粟八斗七分【斗】

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題9:一人斗食,一人半食,一人參食,一人駟食,一人
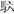
從嶽麓書院藏秦簡《數》看中國早期的衰分問題

從嶽麓書院藏秦簡《數》看中國早期的衰分問題

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
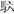
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題10:貣(貸)人百錢,息八

從嶽麓書院藏秦簡《數》看中國早期的衰分問題

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
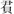
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題11:布八尺十一錢,今有布三尺,得錢幾可(何)。得曰:四錢八分錢一。其述(術)曰:八尺為灋(法),即以三尺乘十一錢以為
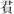
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題12:
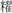
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
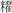
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題13:有金以出三關=,(關)五兌(稅)除金一兩,問始盈金幾可(何)?曰:一兩有(又)六十四分兩之六十一┕。其述(術)曰:直(置)兩而参四之(0832)
算題14:竹【十】節,上節一斗,下節二斗,衰以幾可(何)?曰:衰以幾可(何)?曰:衰以九分斗一。其述(術)曰:直(置)上下數,以少除多,以餘為(0851)衰
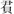
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
算題15:米賈(價)石六十四錢,今有粟四斗,問得錢幾可(何)?曰:十五錢廿五分錢九。其述(術)以粟=(粟米)求之。(0305)
算題16:□□[5]且稟米五斗于倉=,(倉)毋米而有糙=,(糙)二粟一,今出糙幾可(何)當五斗有(又)十三分斗十。倉中有米,不智(知)(0819+0828)
算題17:段(煅)鐵一鈞用炭三石一鈞┕,斤用十三斤┕,兩用十三兩。(0896)
算題18:銅斤十二者
趣味历史故事解说中国历史人物
,兩得十六分十二┕,朱(銖)得廿四分錢十二。(0983)單獨術文1:凡食攻(功)之述(術)曰:以人數為法,以食攻(功)丈數為
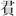
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
單獨術文2:
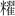
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
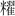
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
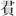
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
其他不能復原為完整算題或術文,但應當屬於此類算題的簡文:

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
分斗六┕,
從嶽麓書院藏秦簡《數》看中國早期的衰分問題

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
曰:以粟為六斗┕,米為十斗┕,麥為六斗【大半】

從嶽麓書院藏秦簡《數》看中國早期的衰分問題
這些算題和術文中包含了一些與《九章》的“衰分”章類似的內容,說明《九章》的“衰分”方法和算題確實很大程度上來自先秦。例如:
算題2與《九章算術》中“衰分”章第一題類似。《九章算術》的算題是:“今有大夫、不更、簪褭、上造、公士,凡五人,共獵得五鹿。欲以爵次分之,問:各得幾何?荅曰:大夫得一鹿三分鹿之二;不更得一鹿三分鹿之一;簪褭得一鹿;上造得三分鹿之二;公士得三分鹿之一。術曰:列置爵數,各自為衰;副并為法;以五鹿乘未并者各自為實。實如法得一鹿。”
算題3與《九章算術》“衰分”章第二題類似。算題3簡文可復原為“一牛一羊一犢共食以禾一石,問牛羊犢各出幾可?曰:牛五斗有七分斗之五,羊出二斗有七分斗之六,犢出一斗有七分斗之三。述曰:牛直四,羊直二,犢直一,而并之。凡求……”[8]。《九章算術》算題是:“今有牛、馬、羊食人苗。苗主責之粟五斗。羊主曰:‘我羊食半馬。’馬主曰:‘我馬食半牛。’今欲衰償之,問:各出幾何?術曰:置牛四、馬二、羊一,各自為列衰;副并為法;以五斗乘未并者各自為實。實如法得一斗。”
算題5與《九章算術》“衰分”章第四題及張家山漢簡《算數書》“女織”算題類似。鄒大海先生指出[9]:“《數》0972簡的問題表述更接近《算數書》,其前面的簡文可能包含諸如‘……織日自再,三日織十尺。問始織日及其次各幾何?得曰:始織一尺七分尺三,次二尺七分尺六,次五尺七分尺’之類的文字。除數字外,其他文字也可以有別的校補方式。”《九章算術》相應算題是:“今有女子善織,日自倍。五日織五尺,問:日織幾何?荅曰:初日織一寸三十一分寸之十九,次日織三寸三十一分寸之七,次日織六寸三十一分寸之十四,次日織一尺二寸三十一分寸之二十八,次日織二尺五寸三十一分寸之二十五。術曰:置一、二、四、八、十六為列衰;副并為法;以五尺乘未并者,各自為實,實如法得一尺。”張家山漢簡《算數書》“女織”算題:“女織 鄰里有女惡自喜也,織曰:自再五日織五尺。問始織日及其次各幾何。曰:始織一寸六十二分寸卅(三十)八,次三寸六十 40 二分寸十四,次六寸六十二分寸廿(二十)八,次尺二寸六十
中国历史之安史之乱的故事
二分寸五十六,次一尺五寸六十二分寸五十。术(術)曰:直(置)二、直(置)四、直(置)八、直(置)十六、直(置) 41 卅(三十)二,并以為法,以五尺偏(遍)乘之各自為實,(實)如法得尺,不盈尺者十之,如法一寸,不盈寸者,以法命分。 王已讎 42 ”算題8應屬於衰分大類中的返衰類問題。它與《九章算術》“衰分”章的“今有甲持粟三升
中国历史故事13岁女孩
,乙持糲米三升,丙持糲飯三升。欲令合而分之,問各幾何?”是完全同型的問題,方法也應是同種方法[10]。算題10《九章算術》“衰分”章第二十題類似,屬返衰類問題。《九章算術》的算題是:“今有貸人千錢,月息三十。今有貸人七百五十錢,九日歸之,問:息幾何?荅曰:六錢四分錢之三。術曰:以月三十日乘千錢為法;以息三十乘今所貸錢數,又以九日乘之,為實。實如法得一錢。”
算題11與《九章算術》“衰分”章第13題相似,但兩者都不是衰分術的問題。
算題12與《九章算術》“衰分”章第14題相似,但兩者都不是衰分術的問題。
算題14是求等差數列公差的問題,此處“衰”相當於等差數列的公差[11]。算題簡文中“十”字殘,依題意、字距、殘痕推斷。據答案“衰以九分斗一”知,需要從“上節一斗”加衰至九次才得到“下節二斗”,連同上節,正好是十節。原簡文“衰以幾可曰”五字抄重了,為衍文,當删。此題中的“除”是減、除去的意思,以少除多,用“上節一斗”减“下節二斗”。 “直(置)節數除一焉以命之”,意為“從竹的節數中減去1,然後以之為分母命名分數”。術文可以表示為算式:
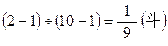
從嶽麓書院藏秦簡《數》看中國早期的衰分問題
《數》裏的算題有衰分術問題和返衰術問題,還有與《九章》衰分章非衰分類問題非常類似的問題,說明《九章》的非衰分問題,亦可能是先秦時期就存在的。
《數》和《算數書》都叫“衰分”而不叫“差分”,說明先秦已有“衰分”之名,雖然先秦亦可能仍有“差分”之名,但漢編本《九章》的先秦祖本可能還是用“衰分”這一名稱,不一定要到漢代才把其“差分”改為“衰分”。
《數》的衰分類問題,可能屬於受經典系統的著作之影響,結合實際需要編寫的問題[13]。
(編者按:[1]郭書春. 九章算術譯注. 上海:上海古籍出版社,2009,P97
[2]鄒大海. 睡虎地秦簡與先秦數學. 考古,2005,(6):57-65
[3]朱漢民,陳松長. 嶽麓書院藏秦簡(貳). 上海:上海辭書出版社,2011本文所引嶽麓秦簡《數》釋文,如無特別說明,均出自該書。
[4]算題10,殘片C410204補入,參見:魯家亮. 讀岳麓秦簡《數》筆記(一). 簡帛網(武漢大學簡帛研究中心網站):http://www.bsm.org.cn/show_article.php?id=1645, 2012-02-25
[5]簡首“□□”兩字疑為“有人”。參見:蕭燦. 嶽麓書院藏秦簡《數》研究. 博士學位論文. 長沙:湖南大學,2010年12月2日. P79
[6]由於簡0898的後續簡文應是“廿七分升十一”,所以整理小組有意見認為第1853號應接第0898號簡,但筆劃殘痕與“廿七分升”字樣不合。參見:蕭燦. 嶽麓書院藏秦簡《數》研究. P75
[7]0840簡首
中国历史人物故事好词积累
殘,現存長度約24.3釐米,下端空白約7.8釐米,上接簡缺失。參見:蕭燦. 嶽麓書院藏秦簡《數》研究. P79[8]算題3的簡編連由許道勝先生於2010年4月22日的整理小組研讀例會提出。算題復原及分析引自:蕭燦. 嶽麓書院藏秦簡《數》研究. P66
[9]關於算題5的觀點出自鄒大海先生於2010年11月28日發給蕭燦的電子郵件,參見:蕭燦. 嶽麓書院藏秦簡《數》研究. P70
[10]關於算題8的觀點出自鄒大海先生於2010年05月24日發給蕭燦的電子郵件,參見:蕭燦. 嶽麓書院藏秦簡《數》研究. P74
[11]引自郭書春先生於2010年11月18日發給蕭燦的電子郵件,參見:蕭燦. 嶽麓書院藏秦簡《數》研究. P78
[12]引自鄒大海先生於2010年4月11日發給蕭燦的電子郵件,參見:蕭燦. 嶽麓書院藏秦簡《數》研究. P78
[13]鄒大海. 先秦數學的兩種傾向. 北京“《算數書》與先秦數學國際學術研討會”報告,2004年8月.鄒大海. 中國數學的興起與先秦數學. 石家莊:河北科學技術出版社,2001 (责任编辑:admin)
原文出处:http://his.newdu.com/a/201711/05/513711.html
以上是关于從嶽麓書院藏秦簡《數》看中國早期的衰分問題的介绍,希望对想了解历史故事的朋友们有所帮助。
本文标题:從嶽麓書院藏秦簡《數》看中國早期的衰分問題;本文链接:http://gazx.sd.cn/zggs/27255.html。
上一篇:讀清華簡《繫年》劄記(一)
下一篇:郭店《成之聞之》23號簡的斷句
猜你喜欢
- 京师大学堂-邯郸学院藏《京师大学堂伦理学讲义》考辨 2023-09-22
- 嘉庆-台北故宫博物院和台北中央研究院藏清代档案概况 2023-09-21
- 冯明珠-冯明珠《河岳海疆——院藏古舆图特展》 2023-09-19
- 陶安:《嶽麓書院藏秦簡(叁)》校勘記 2023-09-07
- 岳麓书院-魯普平:嶽麓書院藏秦簡《為吏治官及黔首》研究綜述 2023-09-07
- 甲子-曲安京、蕭燦:嶽麓書院藏秦簡《質日》曆譜考訂 2023-09-06
- 蕭燦:嶽麓書院藏秦簡《數》贏不足算題研討 2023-09-03
- 讀書會:讀《嶽麓書院藏秦簡(壹)》 2023-09-03
- 文化-小草:《岳麓書院藏秦簡》(壹)考釋一則 2023-09-03
- 中国古代史-讀《嶽麓書院藏秦簡》(肆)札記(二) 2023-08-31


















